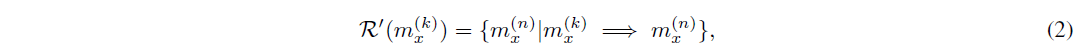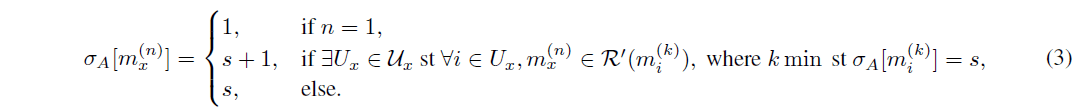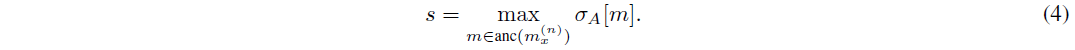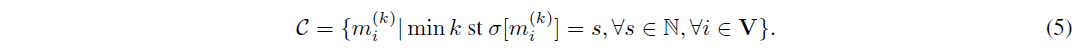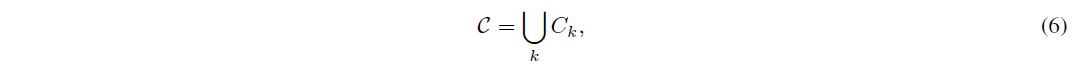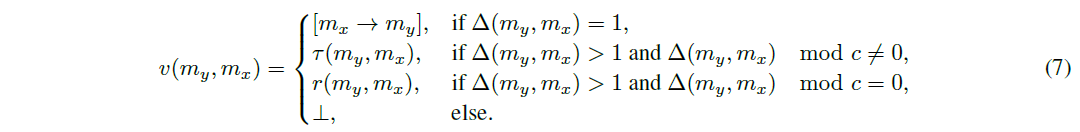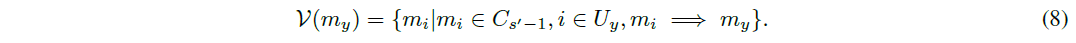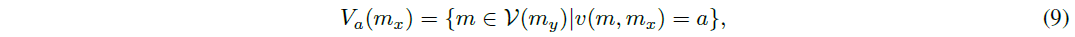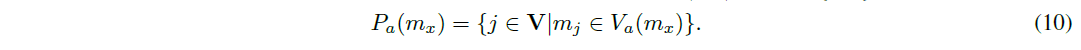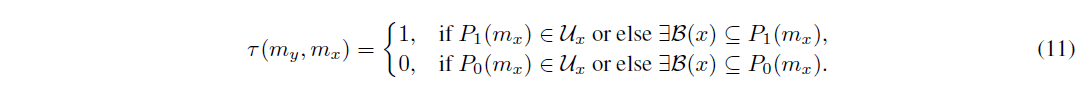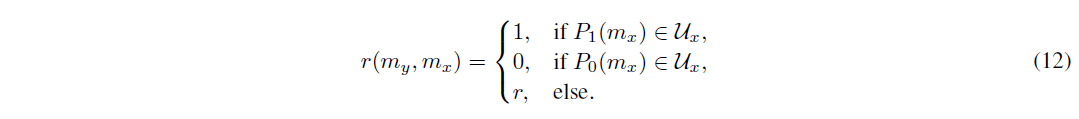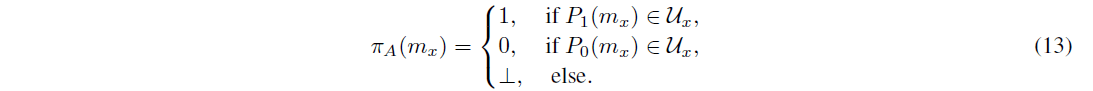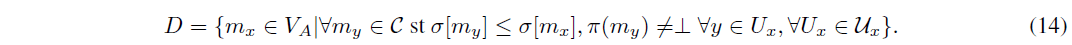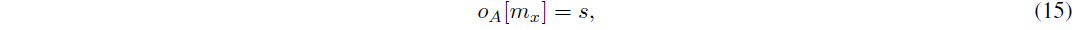FCP(Flere Consensus Protocol)ホワイトペーパー日本語訳

概要

Flare Consensus Protocol (FCP)は、Federated Byzantine Agreement (FBA)コンセンサスの新しい構造です。

FBA構成では、個々の参加者が独立して定足数スライスの決定ができ、ネットワーク上の定足数スライスの決定が重なり、ネットワーク全体のコンセンサスルールが発生するため、コンセンサスを確保するための経済的メカニズムに依存しません。

FCP(Flere Consensus Protocol)はリーダーレスであり、完全に順序付けされているため、攻撃者が2つのトランザクションのうちどちらが最初に順序付けされるかに影響を与えるのは非常に困難です。また、FCP(Flere Consensus Protocol)は非同期であり、Federated Virtual Votingと呼ばれる新しい連合型コンセンサスメカニズムを活用することで、以前のFederated Byzantine Agreement (FBA)の構造よりもはるかにシンプルになっています。

これらの特性により、FCP(Flere Consensus Protocol)はインターネットレベルのチューリング完全合意の有力なモデルとなります。

はじめに

悪意のある参加者が存在する可能性のある分散システムで合意に達する問題は，ビザンチン将軍問題[LSP82]で初めて紹介されました．この問題では、ネットワークの参加者が必ずしも信頼できるとは限らず、このような振る舞いは
これにより、分散システムは、異なる観測者や故障検出システムからは、故障しているようにも機能しているようにも見えてしまうという、より広い意味でのビザンチン故障に該当します。ビザンチン障害ではない参加者間の合意
参加者間の合意を得るためには、メッセージの交換で安全性を確保する必要があります[Bra87]。このようなシナリオでは，ビザンチン型耐故障性アプローチは，サービスを維持するために十分に正しく動作するコンポーネントがあると仮定して，システムサービスの提供の継続性を確保しようとする．言い換えれば、ビザンティン合意は、閉ざされたシステムセット内に特定の割合で誤動作するコンポーネントやメンバーが存在する場合でも、合意を確保できます。

例えば、従来、台帳は完全性を維持するために、中央機関がある取引を受け入れるべきか否かを決定し、その結果、台帳が更新される必要がありました。確かに、参加者は必ずしも正直ではありません。
実際、参加者は必ずしも正直ではないため、あるエンティティがコインを二重に使用してしまうという二重支出の懸念があります。ビットコイン[Nak+08]プロトコルは、ネットワーク上に分散された、暗号的に安全な公開取引台帳であるブロックチェーンを導入しました。ここでは、ネットワークの参加者は、各取引を受け入れるか拒否するか、また取引の順序に同意するかについて合意に達する必要があります。オープンな分散システムにおける合意は、プルーフ・オブ・ワーク[Nak+08]、プルーフ・オブ・ステーク[KN12; DN92]、Federated Byzantine Agreement (FBA)など、さまざまなメカニズムによって達成されますが、それぞれに利点と欠点があります。

二重支出のような悪意のある行動は、より広いビザンチン障害のカテゴリーに入る。これにより、分散システムは、異なる観測者や障害検出システムに対して、予期せずに障害と機能の両方に見えることがある。このような場合
このようなシナリオでは、ビザンチンフォールトトレランス（BFT）[PSL80]アプローチは、サービスを維持するために十分に正しく動作するコンポーネントがあると仮定して、システムサービスの提供の継続性を確保しようとします。
合意を得られます。言い換えれば、ビザンチン合意 [PSL80] は、クローズドシステムセット内に特定の割合で誤動作するコンポーネントやメンバーが存在する場合でも、コンセンサスを確保できます。

proof-of-stake [8]のような純粋に経済学に基づいたブロックチェーンプロトコルに関する緊急の懸念は、中心となる参加者が有限かつ少量の資本、つまりstakeを活用してのみ確保されている場合に、このようなシステムがどのようにしてネットワークの状態で表現される大量の価値をサポートできるかということです。これがトップヘビー・ブロックチェーンの概念です。

Federated Byzantine Agreement (FBA) は、オリジナルのビザンチン合意フレームワークをオープンでパーミッションレスな設定に拡張し、ステークの証明などの安全性を提供する経済的なソリューションによってもたらされるトップヘビーなブロックチェーンのリスクを本質的に回避します。そして、ネットワーク上の参加者に対する信頼の重なりが、ネットワーク全体のコンセンサスのルールを定義します。

つまり、従来のBAが参加者の対称的な信頼を必要とするのに対し、Federated Byzantine Agreement (FBA)は参加者の非対称的な信頼を可能にします。ネットワーク参加者の非対称な信頼性は、各参加者が自分の各参加者は、ネットワークを利用する際の安全性を確保するための独自のルールを定義できます。

例えば、ネットワークの参加者の一部が特定の法的管轄区域に拠点を置いている場合、参加者は地元の規制機関からの表現を安全セットに含められます[SD19]。

Bitcoin [Nak+08]、pBFT (practical BFT) [CL+99]、XRP Ledger consensus protocol [SYB+14]、BFT-CUP [Alc+08]、Stellar Consensus Protocol (SCP)など、様々なコンセンサス方式が開発されており、性能向上のための新たなアプローチが模索されている継続的な研究分野となっています。

例えば、仮想投票は、Hashgraphコンセンサスプロトコル[Bai16]で最初に導入され、その後Blockmaniaコンセンサスプロトコルで活用されている、コンセンサスネットワークの複雑さを軽減する技術であり、広域ネットワーク上の高いトランザクションスループットで非常に高速な最終処理を可能にします。しかし，仮想投票はSybil攻撃の影響を受けやすく，参加者が異なるIDで複数回ネットワークに参加することで，投票手順に悪意のある影響を与えることになります．このため，仮想投票ベースのネットワークでは，Sybil攻撃を本質的に回避できず，proof-of-stakeのようなアドオンメカニズムを導入する必要がある。

本論文では、Federated Byzantine Agreementフレームワークの最新の構成であるFlare Consensus Protocol (FCP)を紹介します。これまでの構成であったStellar Consensus Protocol (SCP) に続くものです。Flare Consensus Protocol (FCP)はSCPに比べて、以下のようないくつかの利点があります。Flare Consensus Protocol (FCP)は、リーダーレス、非同期ビザンチンフォールトトレラント、完全に順序化されたトランザクション、Federated Virtual Votingと呼ばれる新しいネットワークの複雑さを軽減する技術の使用により、高いスケーラビリティを備えています。

さらに、Flare Consensus Protocol (FCP)は連Federated Virtual Voting(仮想投票連合)と呼ばれる仮想投票の新しい一般化であり、従来の仮想投票技術と全く同じようにネットワークの複雑さを軽減しているが、連合ビザンチン協定の枠組みの中で存在により、Sybil攻撃を本質的に克服している。

本論文は以下のように進められる。まず、セクション2では、Federated Byzantine Agreement (FBA)構築に関連する必要な背景定義を紹介します。次に、セクション3では、Flare Consensus Protocol (FCP)を紹介し、最後にセクション4では、Flare Consensus Protocol (FCP)を関連するコンセンサスアルゴリズムと比較する。

Preliminaries(予備工作)

Flare Consensus Protocol (FCP)は、Federated Byzantine Agreement (FBA)のフレームワークに加えて、Hashgraphコンセンサスプロトコル[Bai16]で導入された仮想投票をベースにしています。Flare Consensus Protocol (FCP)は、グラフに関するアイデアに依存しており、それを次に紹介します。

Federated Byzantine Agreement (FBA)の主要なアイデアを紹介し、Federated Byzantine Agreement (FBA)の主要なアイデア、本稿で使用する用語、プロトコルを支えるいくつかの主要な仮定を紹介する。

グラフ理論

グラフG=(V;E)は、頂点Vと有向辺Eの集合で構成されます。有向循環グラフ（DAG）とは、循環のない有向グラフである。頂点u 2 Vからv 2 Vへの有向辺は(u; v)と書きます。が重要となります。u 2 Vからw 2 Vへの長さnのパスは、(vi; vi+1) 2 Eとなるような頂点v0; : : ; vn 2 Vの列である。vi 2 V; i = 0; : : ; n 1のとき、v0 = u, vn = wとなる。このとき、wはvから到達可能であるといい、次のように書かれる。この関係は部分順序を誘導する。すなわち、a ! b と b ! c は a ! c を意味する。

u(u)をu 2 Vの祖先のセットとすると、つまり ancestor(u) = fv 2 Vjv ! ug となる。uの親は、任意の頂点 v 2 Vで、(v; u) 2 Eである。

Federated Byzantine Agreement（FBA）

従来のビザンチン合意ネットワークでは、安全性を確保するために(N-1)/3の故障にしか耐えられません（Nは参加者数）。Federated Byzantine Agreementネットワークでは、この制限は必ずしもなく、ネットワーク全体のクォーラムオーバーラップの特性に応じて、かなりの数のノード障害に耐えられます。この特性により、FBAネットワークはSybil攻撃を本質的に回避できます。なぜなら、ノードは自分が信頼していない悪意のあるノードをクォーラムスライスセットに含めないことを独立して選択できるからです。

ステラコンセンサスプロトコル（SCP）はFederated Byzantine Agreement (FBA)の構築であり、定義2.1を参照し、図1および図2に示されています。これは、他のFBA構築がSCPと同じくらい安全であっても、より安全ではないような最適な安全性保証を達成しています。重要な特徴は、ネットワークの参加者が、クォーラム・スライスと呼ばれる信頼したい他者を選択できることです。これにより、個々のノードが独立してクォーラム・スライスの決定できます。そして、市場原理により、ネットワーク上でクォーラム・スライスの決定が重なり、ネットワーク全体のコンセンサスのルールが発生します。取引は、ネットワーク上の十分な数のノードがその取引を受け入れたときに決済され、これは投票手続きによって達成されます。

定義 2.1. Maz15] FBAS 連合ビザンチン合意システム（FBAS）は、ノードのセットVと定足数関数Q : V ! 22V n f?gは、各ノードに1つ以上のクォーラムスライスを指定し、ノードは自身のすべてのクォーラムスライスに属する（すなわち、8v 2 V; 8q 2 Q(v); v 2 q）。このように、クォーラムは、各ノードが少なくとも1つのクォーラムスライスを含むノードのセットとして定義できます。なお、非連合ビザンチン協定では、すべてのノードが同じスライスを受け入れる必要があるため、クォーラムとクォーラムスライスの間には区別がない。

定義 2.2. Maz15]クォーラム FBAS hV;QiにおけるノードU Vのセットは、U 6= ? かつUが各ノードのスライスを含む場合、すなわち、8v 2 U; 9q 2 Q(v) such that q U.である場合、クォーラムである。

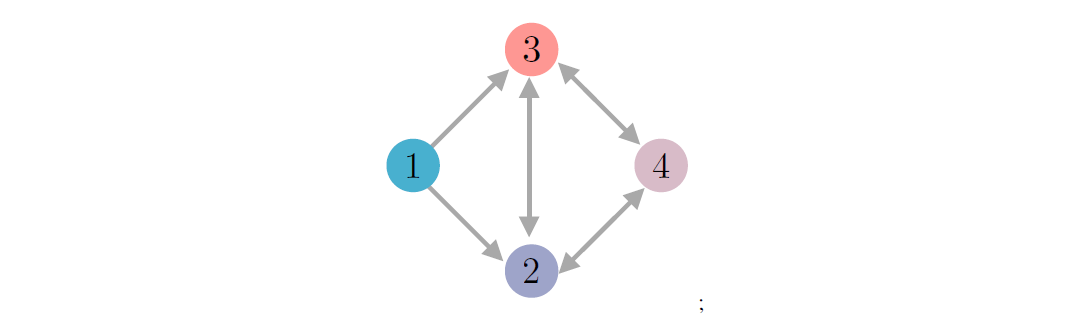
図1：1、2、3、4と書かれた4つのノードを持つFBASの例。矢印は、v 2 f1; 2; 3; 4gの場合、ノードがそのクォーラムスライス関数Q(v)でポイントする別のノードを含むことを表しています。ノード2、3、4はそれぞれ、ノード{2、3、4}からなるクォーラムを持っています。ノード1はそのクォーラムスライスに2と3しか含まれていませんが、両者ともクォーラムスライス内で4に依存しているため、Q(1) = f1; 2; 3; 4gとなります。

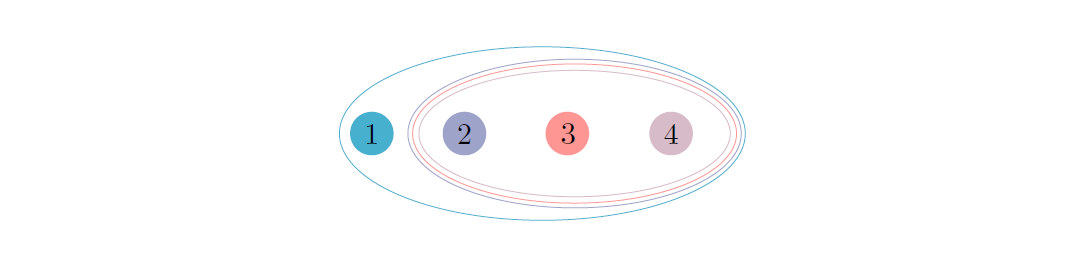
図2：図1に示したFBASの例は、上記のカラースキームを使って代替的に表現できます。ここでは、青く塗られたノード1のクォーラムは、ノード1、2、3、4で構成されており、他のノードについても同様である。

定義 2.3. すなわち、すべてのクォーラム U1 および U2 に対して、U1 ≒ U2 6= ?
定義 2.4. hV;QiをFBASとし、B Vをノードの集合とすると、hV;QiからBを削除する（hV;QiBと書く）ことは、修正されたFBAS hV n B;QBi（QB = fq n Bjq 2 Q(v)g）のを計算を意味する。

ノードのセットは、それを削除してもネットワークの合意形成に支障をきたさない場合、定義2.5を参照して、使い捨て可能なセットDSetと言われます。言い換えれば、DSetの外側にあるノードの安全性とlivenessはそれに依存しない。したがって、理想的なシナリオでは、すべての行儀の悪いノードや故障したノードはDSetに属し、それによってシステムの合意形成能力に影響を与えない。

定義 2.5. Maz15] DSet hV;QiをFBASとし、B Vをノードのセットとする。以下の場合、BはDispensible Set (D-Set)であるという。
(1) (Bにもかかわらずクォーラムが交差している) hV;QiBはクォーラムが交差している。
(2) (Bにもかかわらずクォーラムが存在する) V n BがhV;Qiのクォーラムであるか、B = Vのどちらかである。

一方、与えられたセットが与えられたノードのクォーラムスライスのそれぞれに属している場合、それはv-ブロッキングであると言われます。

定義 2.6. [Maz15]v-ブロッキング。v 2 VをFBAS hV;Qiのノードとする。集合B Vは、それがvのスライスのすべての1つをオーバーラップする場合、v-ブロッキングである。
すなわち、8q 2 Q(v); q \ B 6= ?

ノードの用語

分散環境では、システムの正しい機能を破壊しようとする悪意のある行為者が大きな問題となります。しかし、悪質な行為者はどのようにして形式的に定義されるのでしょうか。この問題を解決するために、善良な行為者の行動を表す「well-behaved」（正直者と呼ばれることもある）という概念が導入されています。非公式には、善良な行為者は非公式に分別ある行動をしなければなりません。つまり、プロトコルに従うこと、自分のクォーラムスライスに関して適切な選択をすること、要求に応えることです。そうでなければ、お行儀が悪く、ビザンチン障害になると言われています。

プロトコルの時間経過に伴い、参加者が更新の適用が目標となりますが、これをスロットと呼びます。次に、ノードvは、まずスロットiが依存しているすべての依存関係に更新を適用し、次に、他のすべての正しく機能しているノードも更新を適用すると信じている場合、スロットi（スロットは、例えば、元帳のトランザクション番号）に更新xの適用を決定します。この場合、vはスロットiに対してxを外部化したという。

定義 2.7. Maz15]安全性 FBASのノードのセットは、2つのノードが同じスロットで異なる値を外部化がなければ、安全性を享受できます。そうでない場合は発散する。

定義 2.8. FBASのノードセットは、失敗した（行儀の悪いノードを含む）ノードの参加なしに新しい値を外部に出せれば、有効である。そうでない場合は、ブロックされる。

定義 2.9. お行儀の良いノードは、安全かつ生きている場合、正しいと言う。それ以外の場合は失敗となる。

定義 2.10. Maz15] intact ノードvは、すべての行儀の悪いノードを含むDSet Bが存在し、v 62 Bである場合、intactであるという。

最後に、かつて誠実であったノードが悪行を働くようになることも、その逆もあり得ることに注意してほしい。

前提条件

このプロトコルは、いくつかの共通の仮定に基づいています。1つ目は、メッセージの偽造が不可能であることです。

仮定2.1. ノードが相互に送信するメッセージは偽造できない。すなわち、ノードは公開鍵で名前が付けられており、暗号的に安全なデジタル署名を使用している。次に、非同期システムでは、メッセージは遅れても最終的には届くということが一般的に想定されています。ただし、メッセージが届く順番は、必ずしも送信された順番とは一致しません。

想定2.2. ネットワークは、お行儀の良いノード間では、メッセージが任意に遅延したり、順番が変わったりしても、最終的にはメッセージを配信します。

最後の仮定は、クォーラム・スライスの存在を保証するものです。仮定2.3. DSetを削除した後、すべてのノードのクォーラムが交差する。以上で予備セクションを終了します。次のセクションでは、Flare Consensus Protocol (FCP)の紹介と分析を行います。

Flare Consensus Protocol (FCP)

グローバルグラフの生成

ネットワークはN個のノード（以降、曖昧さをなくすためにパーティシパントと呼ぶ）の集合で構成され、これらは集合V（jVj=N）で表される。パーティシパントの集合に対してクォーラム関数Qが定義され、これらはFBAS hV;Qiを形成する。Uをすべてのクォーラムの集合とし、より具体的にはUx = fU 2 Ujx 2 Vgを参加者x 2 Vのクォーラムの集合とする。

参加者は、お互いに任意のトランザクションを実行したいと考えており、重要なのは、ネットワークの整合性を維持するために、これらのトランザクションを順序付けることです。以下では、例示のために、金融取引という特定のケースを使用する。Flare Consensus Protocol (FCP)は、あらゆるタイプのステートフルな決定論的トランザクションを処理する一般化されたプロトコルであることに留意が重要である。

例えば、アリス(参加者A 2 V)がボブ(参加者B 2 V)にトランザクションを送信したいとする。実際には、アリスが、他の情報に加えて、ボブに送りたい金額を含むメッセージ作成で実現する。次に、参加者が取引の順序に同意するためには、この情報をできるだけ効率的にすべての参加者に伝達する必要があります。これがコンセンサスの問題であり、Flare Consensus Protocol (FCP)では、広く共有されたメッセージ、すなわち多数の参加者に伝達されたメッセージに対する投票手続きによって達成されます。

このように、メッセージは作成、送信、受信のいずれも可能です。例えば、プロトコルの開始時、アリスが作成した最初のメッセージはm(1)Aと呼ばれる。 情報が他の参加者に伝達され、グローバルな知識となるために、ゴシッププロトコルが実行される。ここでは、アリスは残りの参加者に対する確率分布p()に従って、別のノードを選ぶ。最も単純なケースでは、残りの参加者全員に対する一様な確率分布である。例えば、AliceはCharlie（参加者C 2 V）を選び、彼にメッセージ
m(1)A 。

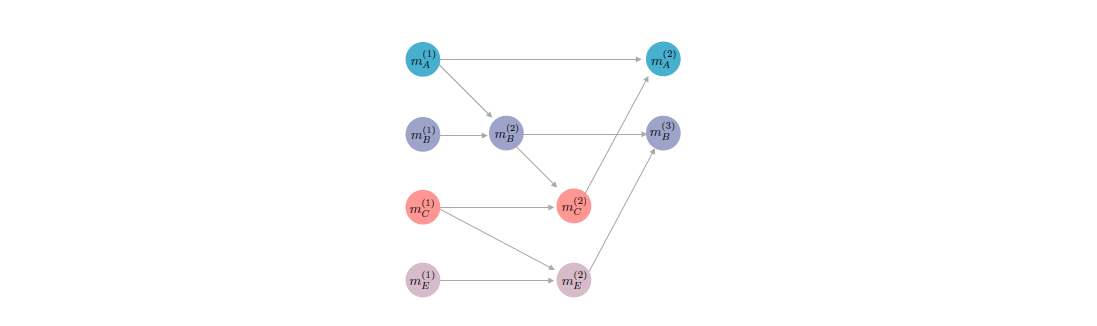
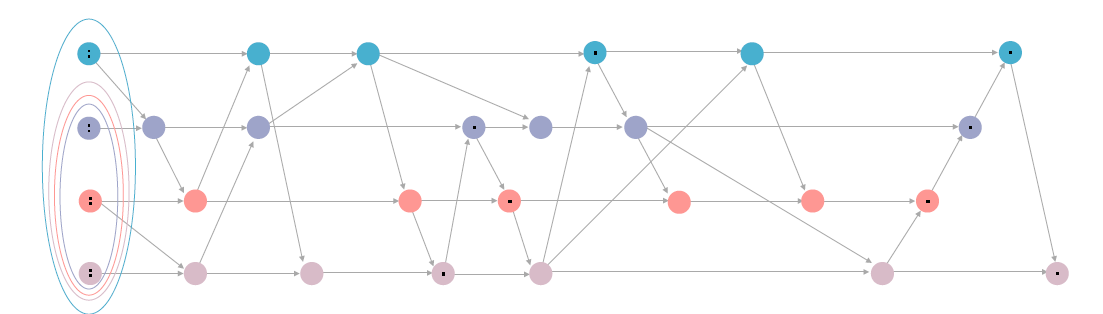
このメッセージを受け取ったCharlieは，例えばMerkle木で行われているように，受け取ったメッセージに関する情報と，自分が最後に作ったメッセージに関する情報を含む新しいメッセージを作らなければならない．この新しいメッセージの作成は、このメッセージ・ロードにトランザクションを添付するチャンスでもあり、それをゴシップ・プロトコルを介して伝播します。参加者間のメッセージの作成と伝播は、DAGで表現されます。ここで、頂点はメッセージを表し、有向エッジは、ある参加者から他の参加者にメッセージが送信され、その結果、新しい頂点が作成されることを表します。図3は、メッセージの流れの一例です。

ここで、Vはメッセージを表す頂点の集合、Eはメッセージ間のつながりを表す辺の集合を表しています。このDAGには、各参加者が通信、受信、作成したメッセージの履歴が含まれています。しかし、どの参加者もこの情報に直接アクセスできません。実際、参加者は、自分が受け取ったメッセージと、その中に含まれる履歴に関連する追加情報しか認識できません。このため、各参加者はこの部分的な情報を、定義3.4のローカルDAGとして表現します。このプロトコルは、各参加者がこのローカルな構造を構築し、これらのメッセージを順番に並べるために、3.8節のFederated Virtual Voting(仮想投票連合)手順実行で構成されています。

Messages

具体的には、メッセージは、2つの親のハッシュ、トランザクション、作成者のクォーマスライス関数のハッシュ、デジタル署名の5つのフィールドでラベル付けされたデータ構造である。これら5つのフィールドがメッセージを一意に決定する。

定義 3.1. メッセージ メッセージm(n)x 2 Vは、パーティシパントx 2 Vが作成したn番目のデータ構造であり、以下の内容で構成される。

ここで、Hash(x)は、暗号的に安全なハッシュ関数を示し、Sign(m(n) x ）は，メッセージ認証のためのデジタル署名方式を示す。

図3：4人の参加者によるコンセンサス・アルゴリズム内のメッセージ・フローの例で、メッセージは時間的に左から右に向かって流れる。ここでは、4人の参加者（A;B;C;E）がいて、それぞれがクォーラムスライスを持っています。このシステムでは、メッセージm(2)Bの祖先はメッセージfm(1) A ;m(1) B gであり、メッセージm(2)Aの祖先はfm(1) A ;m(2) C ;m(1) C ;m(2) B ;m(1) B gである。メッセージm(2)Aの親はm(1)Aとm(2)Cである。

定義 3.2. 初期メッセージ 初期メッセージ（n = 1の場合）は，プロトコルの開始時に参加者が作成する最初のメッセージである。

例えば、参加者x 2 Vが作成したメッセージは、mxと呼ばれることがあります。

1人の参加者が2つのメッセージを作成し、どちらにも相手の情報が含まれていない場合、二重支出やその他の悪意のある行動が発生する可能性があります。これをフォークと呼びます。

定義 3.3. フォーク メッセージのペア(m(n)x ;m(k)x )は、m(n)xとm(k)xが同じ参加者x 2 Vによって作成されたが、どちらも相手の祖先ではない場合、フォークとなります。より一般的には、Fxは、任意のx 2 Vについて、参加者xによって作成されたすべてのフォークのセットを表すとする。なお、定義上、お行儀の良いノードはフォークを作成しない。

局所的なグラフの生成

しかし、各参加者は、特定のメッセージと、DAGで表されるネットワーク履歴の一部しか認識していません。Gxを参加者x 2 VのDAGとし、Vxを参加者xのDAGのメッセージの集合、つまりDAGの頂点とします。
xのDAGのメッセージの集合、つまりDAGの頂点を表します。

したがって、例えば、アリスは自分が受け取るメッセージと、それに含まれる情報を認識しており、それは、ハッシュの二分木であるMerkle tree [Mer87]と同様に、祖先のハッシュを介してネットワークの履歴に関する情報を含んでいます。彼女が認識している情報は、ローカル・グラフGAで表される。この情報は、ネットワークに関する他の参加者（例えばボブ）の知識（DAG GBで表される）とは異なる可能性がある。

定義 3.4. ローカルグラフ 各参加者x 2 Vは、DAG Gx = (Vx;Ex)であるローカルグラフを生成する。これは、参加者xが認識しているメッセージの集合に対応する頂点Vx = fm(k) i ji 2 V; k 2 Ngと、有向エッジEx = f(m(k) i ;m(k0) j )ji; j 2 Vx; k; k0 2 Ngからなり、(mi;mj)はメッセージm(k)iからm(k0)jへの有向エッジである。

グラフの整合性

このように、ローカル・グラフには、グローバル・グラフの部分的な情報が含まれており、より具体的には、Vx V . 時間の経過とともに、より多くのメッセージが参加者間で共有されるようになり、参加者のローカル・グラフは次第にグローバル・グラフを反映するようになっていきます。このメカニズムにより、各参加者は自分のローカルDAGにローカル投票手順を実装できるようになります。

2つのローカルDAG、例えばGAとGBがあると、それぞれの特定の頂点は同じメッセージを表しています。これを正式に定義すると以下のようになります。

定義3.5. 同一のメッセージ 2つのローカルグラフGAとGBが与えられたとき、x; y 2 Vに対する2つのメッセージm(n) x 2 VAと~m(n) x 2 VBは、同じペイロードだけでなく、同じ3つのハッシュとデジタル署名を含んでいる場合、同一であると言います。そして、そのメッセージは両方のグラフに出現すると言われています。これにより、一貫性のあるグラフという概念を導入できます。

定義 3.6. 一貫性のある2つの局所グラフGAとGBは一貫性があり、GA = GBと書きます。これは、z 2 Vについて、2つの同一のメッセージm(n) z 2 GAと~m(n) z 2 GBがある場合、両方とも同じ祖先のセットを含み、それらの祖先の間に同じ親エッジがある場合です。

次のLemmaは、個々の参加者が保持するローカルデータ構造、すなわちDAGがすべてこの一貫性の特性を満たすことを示しています。Lemma 3.1 (一貫性のあるDAG). すべての参加者は一貫したローカルDAGを持っている。

証明します。メッセージm(n)xが2つのローカルDAG GAとGAの両方に含まれるとします。定義3.5により、これは両方のメッセージが同じ3つのハッシュを含み、特に両方の親のハッシュが同じであることを意味します。これは、両方のグラフにm(n)xの親が含まれていることを意味します。 暗号ハッシュ関数は安全であると仮定されているため、つまり衝突がないため、親は同じでなければなりません。帰納法により、m(n)xのすべての祖先はGAとGBで同じでなければならず、一貫性の条件1を満たす。仮定により、2番目の条件が満たされます。したがって、GAとGBは整合性があります。

グラフの接続性

ローカルDAGが構築されると、参加者は、トランザクションの順序に関して合意に達したいと思うでしょう。これは、参加者の間でより広く伝達され共有されているという意味で、他のメッセージよりも重要であると考えられるメッセージの考慮で達成されます。これは、ローカルグラフの連結性、すなわち頂点の到達可能性の度合いによって決定されます。

フォークの存在は、システムの完全性を脅かす可能性がある。したがって、メッセージのローカルDAGの文脈では、頂点の到達可能性の定義は、この点を考慮して修正されています。定義 3.7. 到達可能 以下の場合、メッセージmxは、VA内のメッセージmyから到達可能であるといい、my ! mxと書きます。

局所グラフが与えられたとき、頂点uから頂点vへのすべてのパスのうち、vの作成者によるフォークを含まないパスの集合をPu!vとすると、jPu!vjはそのようなパスの数を表します。直感的には、2つの頂点を結ぶパスが多ければ多いほど、その2つは強く結ばれていることになります。これらを理解するために、強い到達可能性が導入され、2つの頂点が十分な数のパスで接続されているだけでなく、さらに十分な数の関連する参加者を経由していなければなりません。より正確には、2つの頂点uとvは、vのクリエーターの頂点の定足数を経由するパスによって接続されなければならない。

定義 3.8. 強く到達可能 以下の場合、メッセージmxは、メッセージmyによって強く到達可能であると言う。

さて、メッセージmxが与えられたとき、mxから強く到達可能なすべてのメッセージの集合を考えられます。

このセットには、同じクリエーターからの強く到達可能な頂点のみを考慮するような制限を加えられます。

ここで、R0(mx)R(mx)。

次に、行儀の悪い参加者xがフォークを作ってしまった場合を考えます。この場合、2つの一貫したローカルグラフはどのような結果になるでしょうか？次のLemmaは、参加者がフォークを作った場合、次のラウンドでメッセージに強く到達できるのは、これらのメッセージのうちの1つだけであることを教えてくれます。

Lemma 3.2 (strong reachability). 2つの一貫した局所グラフGAとGBを考え、参加者x 2 Vがフォークを作ったと考える (m(n) x ;m(n0) x ) 。さらに、mz 2 VAを無傷のノードからのメッセージs.t. m(n) x =) mzとする。すると、m(n0) x =6) mj , 8mj 2 VBとなる。

証明は矛盾によるもので、すなわち、mj 2 VB st m(n0) x =) mj というメッセージが存在すると仮定する。強く到達するの定義により、これは、9Uj 2 Uj st m(n0)x ! ml and ml ! mj , 8ml 2 Uj . さらに、仮定により、m(n) x =) mz となり、ここで、m(n)x ;mz 2 VAとなる。強い到達可能性の定義の(2)により、次のような定足数が存在する。
Uz 2 Uz st 8i 2 Uz;m(n) x ! mi and mi ! mz. 仮定GA GBのように、DSet Bを削除した後、すべてのクォーラムはクォーラム交点を持つ。DSetの定義により、hV;QiBはクォーラム交点を持つ。さらに、cはwell-behavedである。また、mc 2 VAと~mc 2 VBを、この参加者がローカルグラフに作成したメッセージとすると、m(n0) x ! ~mc および ~mc ! mj とし、m(n) x ! mc および mc ! mz とする。ここで、well-behavedの定義により、(mc; ~mc)はフォークではないので、一方が他方の祖先になります。mcを祖先とすると、したがってmc ! ~mcとなります。したがって、m(n) x ! mc と mc ! ～mcとなります。したがって、m(n)xは~mcの先祖である。しかし，m(n0) x ! ~mcである。なので、m(n0) x と m(n) x の両方が ~mc の先祖である。仮定により、(m(n)x ;m(n0)x ) はフォークであるため、m(n0)x !6 m~ c となり、それゆえ矛盾が生じます。

スロット番号

Strongly reachable messagesは、メッセージの集合に部分的な順序を導入しています。具体的には、プロトコルの開始時に、初期メッセージが作成されます。より多くのメッセージが作成され、送信されると、その中には広く到達可能なもの、つまり以前のメッセージとより強く接続されたものが出てきます。与えられたローカルDAG GAにおけるメッセージの広がりと接続性を追跡するために、メッセージスロット番号A[m]が導入されています。プロトコルの開始時には、各メッセージは最初のスロットに入っています。すなわち、A[m(1) i ] = 1, 8i 2 V. ここで、m(n)xをm(1)xから同じクリエーターで強く到達可能な最初のメッセージ、すなわちm(n)x 2 R0(m(1)x )とします。さらに、m(n)xは、xの定足数を形成する初期メッセージのセットから強く到達可能であるとします。この場合、メッセージm(n)xのスロット番号は1つ増加します。これらの条件が満たされていない場合、スロット番号は単にメッセージの親の最大スロット番号となり、この場合は1となります。

定義 3.9. スロット スロット番号 A[mx] : mx 2 VA ! N, x 2 V, A 2 V, は次のように定義されます。

そしてメンバーは常に一貫したローカルグラフを持っていることを思い出してください。次のLemmaは、あるメッセージが2つのローカルグラフに含まれている場合、各参加者がそのスロット番号に同意を保証しています。

Lemma 3.3 (一貫したスロット). GAとGBをメッセージm(n)xを含む2つの一貫したローカルグラフとすると、両者はm(n)xに作成された同じスロット番号を割り当てる、すなわち、A[m(n)x ]=B[m(n)x ]となる。

証明 前提として、GAとGBの両方にメッセージm(n)xが含まれています。 GA GBとして、整合性の定義により、両方とも同じ祖先のセットを含み、これらの間に同じ親エッジがあります。これには、最初に作成されたメッセージが含まれます。

両方のグラフは、その最初のメッセージのスロット番号に同意しており、それは定義により1です。ここで，両方のグラフに属する任意のメッセージをmyとします。次に、スロットsのコアメッセージから強く到達できるような参加者の定数Uy 2 Uyがスロットsに存在するかどうかを判断する必要がありますが、祖先集合のグラフ接続性は同じなので、両グラフはmyのスロット番号について同意するでしょう。
のスロット番号で一致します。したがって、両グラフは、mxを含む、共有するすべてのメッセージのスロット番号に同意になります。

つまり，すべての参加者A 2 Vについて，[x]はA[x]と書きます。

コアメッセージ

このように、スロット番号の定義からすると、各スロットで最初に作られるメッセージのセットが特に重要になります。これらはコアメッセージと呼ばれています。定義 3.10. コアメッセージ コアメッセージの集合は次のように定義される。

さらに、コア・メッセージmxがフォークでない場合、そのメッセージはユニークであると言われます。
次に、コア・メッセージのセットは、各スロット番号に応じて分離されたセットに分割されます。

ここで、Ci = fm 2 Cj[m] = igとする。さらに、(m; n) = [m] [n]について紹介します。次のステップは、強く到達したメッセージの重要性について、参加者が合意に達することです。これは、Federated Virtual Voting(仮想投票連合)の手順によって達成される。

Federated Virtual Voting(仮想投票連合)

概要

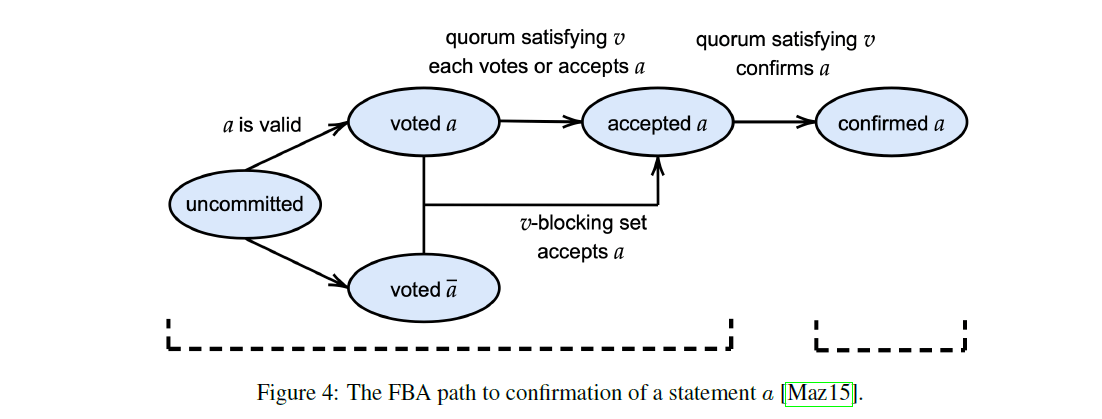
各参加者がそれぞれのローカルDAGを構築したところで、メッセージの順序について合意に達することが目標となります。これは、Federated Virtual Voting(仮想投票連合)アルゴリズムによって達成され、投票プロセスを通じて、特定のコアメッセージがピボットであると決定されます。図4は、ステートメントaの確認までの流れを示しています。

次に、これらが評価されると、メッセージにオーダー番号が割り当てられ、すべてのメッセージがオーダーされ、コンセンサスが得られるようになります。

投票

このプロトコルは、各参加者が投票手順の実行で成り立っており、各コア・メッセージは、前のコア・メッセージの接続性に関して、投票機能を介して投票を行います。例えば、あるコア・メッセージ my は
前のスロットのコア・メッセージmxに投票します（各参加者が各ラウンドで1つのコア・メッセージを持つことを思い出してください）。投票された票は、定義3.12の投票関数によって決定され、このプロセスは選挙と呼ばれる。

定義 3.11. 選挙 選挙とは，投票関数の評価，すなわち，1つのコアメッセージが前のスロットのコアメッセージに投票した結果を意味します。

投票関数はまず、連続するスロットの2つのコア・メッセージについて定義されます。myがmxから到達可能であれば、myはYesを投票し（a＝1）、そうでなければNoを投票します（a＝0）。メッセージmyとmxが複数のスロットで区切られている場合、投票は前のスロットで投票された票を集計するtally関数（定義3.14参照）によって実装されます。これは、定義3.13の投票者セットを構築し、その投票の集計によって行われます。投票メッセージ（myとします）が、自分の投票者セットが投票されるメッセージの定足数であり、これらがすべて同じように投票していることを発見すると、myもそのように投票します。このような決定がなされると、myはさらに、定義3.15のpivot関数の評価を通じて、mxをpivotと決定します。最後に、投票機能では、投票手順の終了を保証するために、コインフリップが導入されています。

定義 3.12. 投票 投票関数 v(my;mx) : C C ! f0; 1; ?g は次のように定義される。

ここで、[P]は文Pの真偽、(my;mx)は11で定義されたタリー関数、r(my;mx)は12で定義されたランダマイズ関数、? はコミットされていない状態、c 2 Nはコインフリップを意味します。

投票機能は、少なくとも2つ以上のスロットで区切られたメッセージの投票を集計するtally関数に依存しています。すなわち、この場合、s 2 Nに対して、[mx] = sならば、[my] = s0 s + 2となります。ここで、メッセージmyは、関連する、すなわちyの定足数に含まれる、前のコア・メッセージの投票を集計する必要があります。
quorumの中で，前のスロットのコアメッセージからの投票を集計する必要があります。これらのメッセージを「投票者セット」と呼びます。

定義 3.13. 投票者セット スロットs0におけるコアメッセージ（および投票者）myの投票者セットは次のように定義されます。

さらに、myの投票者セットV(my)は、次のように分割できます。 V (my) = V1(mx) [ V0(mx), ここで

ここで、aは2 f0; 1gです。これらのセットは、スロットs0のメッセージmyに依存することに注意してください。
次に，a 2 f0; 1gの場合，Va(mx)に属するメッセージを作成した参加者を考えます。

これにより、タリー機能は次のように定義されます。

定義 3.14. Tally タリー関数(my;mx) : C C ! f0; 1g を定義する。

ここで、B(x)はx-blocking集合であり、定義2.6を参照。

最後に、コインフリップの場合、ランダム化関数r(my;mx) : C C ! f0; 1gは次のように与えられる。

ここで，rはmyの署名の中間ビットである。このようにして、投票手順の第一段階が定義されます。

受け入れ

次の段階では、特に重要なコア・メッセージであるピボット・メッセージが導入されます。

定義 3.15. ここで，A : C ! f0; 1g は，ピボット関数である。 と定義される。

このように、ピボット・メッセージには、vote関数とtally関数の両方が計算されていることが必要です。ピボット・メッセージはコア・メッセージであると定義されていることに注意してください。Pをすべてのピボットの集合とすると、コアメッセージと同様にP = [Pi, where
Pi = fm 2 Pj[m] = i; i 2 Ng. 図5は、5人の参加者のDAGの例で、コア・メッセージとピボットの両方が計算されています。

図5：コンセンサス・アルゴリズムにおけるメッセージ・フローの例。黒点が1つの頂点はコア・メッセージ、黒点が2つの頂点はピボットと判定されている。

このように、あるコア・メッセージに関して、コア・メッセージの定足数が同一の投票を行うと、合意に達したとみなされ、選挙には結果が出る。このように，参加者はどのコア・メッセージがピボットであり，どのコア・メッセージがピボットでないかについて合意に達します。
そうでないもの

定義 3.16. 選挙結果 選挙は，前のスロットのコアメッセージがピボットであるかないか（ピボットであればa＝1，そうでなければa＝0）が決定されたとき，スロットsで結果aを持つ。

定義 3.17. 決定 コアメッセージがピボットであるかないかが決定されたとき、選挙は決定されたという。これはビザンチン合意として知られている。

コア・メッセージは、前のコア・メッセージがピボットであるかどうかを評価します。先験的には、異なるコア・メッセージが異なる結果をもたらす可能性があります。つまり、特定の投票者セットに応じて、与えられたメッセージがピボットと評価されたり、そうでなかったりする可能性があります。次のLemmaは、そのようなことはなく、ある有権者セットに対してコア・メッセージがピボットであると判断されれば、他の有権者セットも同じ結論に達することを示しています。

Lemma 3.4. (Consistent voting) GAとGBを2つの矛盾のないローカルグラフとする。GA上で実行されるアルゴリズムは、ある選挙において、スロットsのコアメッセージmxがスロットs + 1のコアメッセージmyに投票ax 2 f0; 1gを送ることを示すとする。そして，GB上で動作するアルゴリズムが，スロットsのコアメッセージ~mxが，スロットs + 1の証人~myに投票~ax 2 f0; 1gを送信することを示すとする。すると，ax = ~axとなります。

証明します。mx 2 VAと~mx 2 VBを考える。第1の選択肢は、(mx; ~mx)がxによって作られたフォークであるということです。 Lemma3.2により、これらのメッセージのうち1つだけが他のメッセージに強く到達できます。しかし、前提として、メッセージmxと~mxの両方が投票を送信している、つまり、両方ともmyに強く接続されていなければならず、したがって、矛盾が生じてしまいます。したがって、これは、xによって作られたメッセージの1つが他のメッセージの祖先であることを意味する。しかし、これらは前提としてコア・メッセージであり、したがって最小のスロット番号を持たなければならない。
つまり、これらは同じものであるということです。したがって、この2つの投票は、両方のグラフで同一のメッセージmxから来ているはずです。メッセージが送る投票は、純粋にその祖先の関数として計算されます。2つのグラフが一致しているので、これらは
同じであるため、2つのグラフは投票に関して一致しているはずで、ax = ~axとなります。

このように、異なるコア・メッセージは、前のコア・メッセージのピボットの性質に関して、同じ結論に達します。さらに、次のLemmaにより、最大でも互いに2スロット以内にこの結論に達することが保証されています。

Lemma 3.5 (Consistent decisions). GAとGBを2つの一貫したローカルグラフとする。そして、GAがスロットsで結果がaの連合ビザンチン合意選挙を決定し、GBがs以前に決定していないとすると、GBはスロットs+2かそれ以前にaを決定する。

証明。前提として、GAはスロットsでa 2 f0; 1gという結果の連合ビザンチン合意選挙を決定した。これは、それより前のスロット、すなわち[mx] < sにコアメッセージmxが存在し、それがスロットsでピボットであるか否か、すなわち(mx)=aと決定されることを意味する。

Lemma3.4により、整合性のあるグラフでは、同じスロットの同じクリエーターからのコアメッセージは、同じように投票されます。送られた投票は純粋に祖先に依存していることを思い出してください。したがって，定足数全体も，両方のグラフのすべてのコアメッセージにaを送ることになります。一貫性の定義により、DSetを削除した後、GAとGBのすべてのクォーラムはクォーラムの交点を持ちます。したがって、GAとGBの両方のスロットsにあるすべてのコアメッセージはaに投票になります（一部の人はaを決定するかもしれません）。そして、スロットs＋1が通常のスロットであれば、そのスロットにあるGAとGBのすべてのコアメッセージが全会一致でaに投票し、aを決定します。スロットs＋1がコインフリップであれば、全員が全会一致でaに投票するので、無作為抽出にはならず、全員がaに投票し、その後、スロットs＋2で全員がaを決定します。

このようにして、ある参加者が以前のコアメッセージのピボット状態に関する結論を出した場合、その直後に定足数が交差している参加者全員が同調が保証されます。しかし、あるコア・メッセージがコア・メッセージが未決定のピボット・ステータスを維持している可能性はあるでしょうか？次の定理は、この疑問に否定的に答えます。定理3.6（ピボット計算）。ピボット関数は最終的に確率1で決定される。

証明 あるコアメッセージmzを考える。Lemma3.5により、ある参加者xがmzがピボットであるかどうかを決定した場合、すなわちa 2 f0; 1gについて(mz) = aと決定した場合、xと定足数が交差するすべての参加者は2スロット以内に同じように決定します。つまり、mxのピボット状態が未決定のまま、つまり(mx)=?
なぜなら、どのコアメッセージも全会一致の定足数を得ることはないからです。しかし、コインフリップでは、そのような定足数がまだ達成されていない場合、すべてのインタクトノードがランダムに投票を選択し、全員が同じ投票を選択する非ゼロの確率を持つことになります。cスロットごとにコインフリップが行われ、コインフリップは永遠に定期的に発生するため、最終的には無傷のノードが確率1で全会一致となり、lemma 3.5により2スロット以内にコンセンサスが得られます。

コアメッセージは、投票関数と投票者セットを介して、以前のコアメッセージのピボット関数の値を決定します。次のLemmaは、あるコアメッセージがpivotであるかどうかが数スロット以内に決定されることを保証しています。

Lemma3.7（ピボットの存在）。任意のスロット番号sに対して、参加者zが作成したスロットs＋3のメッセージmzを少なくとも1つ持つ任意のローカルDAGについて、スロットsにはピボットと決定されるコアメッセージが少なくとも1つ存在し、この決定は、スロットs＋3のzと定足数が交差する参加者からのすべてのコアメッセージ、またはそれ以前に行われる。

ローカルDAGの1つを考え、s 2 N st mz 2 Cs+3とする。次のようなコアメッセージのセットを考える。 Si = fmx 2 Cijmx =) my;my 2 Ci+1g (i < s + 3)。Sy 6= ? "とすると，強到達性の定義により，スロットiにはUy 2 Uy st mz ! mi;mi ! my, 8i 2 Uyが存在します。強い到達可能性は到達可能性を意味するので、Ss+1にメッセージを持つ各参加者は、Ssのメッセージの定足数に到達していることになります。さて、lemma 3.2により、参加者の誰もが、強到達性を持つ与えられたスロットに複数のコア・メッセージを作ることはできません。スロットi + 1にコア・メッセージが存在すると、ノードの定足数がスロットiで強く到達していることが保証され、参加者の誰もが、強く到達している与えられたスロットで1つ以上のコア・メッセージを作成できません。仮定により、mzはs + 3のコアメッセージである。したがって、Siのすべてのクォーラムはz, 8 i s + 2とクォーラム交点を持つ。

さらに、強い到達可能性は到達可能性を意味するので、Ss+1にメッセージを持つ各参加者は、Ssのメッセージのクォーラムから到達できます。Ss+1内の定足数には定足数交差の性質があるため、Ss内にはSs+1の参加者の定足数に到達するSsのメッセージ（mxと呼ぶ）が少なくとも1つは存在しなければならない。

これは、Ss+1のコアメッセージのクォーラムは、それぞれSsのメッセージのクォーラムに到達するからであり、Ssには少なくとも1つのメッセージを含むv-ブロッキングセットは、Ss+1のクォーラムからすべてのコアメッセージに到達する少なくとも1つのメッセージを含むSsに存在しなければならない。したがって、Ss+1内の参加者の定足数は、mxをピボットとする選挙で賛成票を投じることになる。したがって、Ss+2内のすべてのメッセージは、システム全体のステータスをイエス・ヴァレントにする、mxがピボットであるかどうかのイエス投票のvブロックセットを少なくとも受け取り、mxがピボットであるかどうかを投票になります（mxがピボットであると決定してもしなくてもよい）。

したがって、Ss+3のメッセージは、mxがピボットであるという全会一致の投票を受けることになり、それによってmxがピボットであると決定になる。
したがって、スロットs＋3にxとの定足数交点を持つメッセージを持つすべての参加者は、まずスロットs＋2またはs＋3のいずれかでmxがピボットであると決定する。

後に、次のLemmaでは、DAGに新しいメッセージを追加が、与えられたスロットのピボットのセットに与える影響を考えます。

Lemma 3.8 (新しいピボットなし). GAを、メッセージmxを含まないがmxの全ての祖先を含むようなものとし、GAにmxを追加した結果をG0 Aとします。さらに、mxをスロットsで作成されたコアメッセージとし、GAにはスロットsでピボットまたはピボットでないと決定されたコアメッセージが少なくとも1つあるとします。すると、G0 Aではmxはピボットではないと決定されます。

証明 仮定により、スロットsのGAには、スロットsのコアメッセージがピボットであるかどうかを決定するコアメッセージ（mw 2 Csとする）が存在する。mx =2 GAであるため、mwの祖先のどれもmxからは到達できません。mx以外のすべてのメッセージは両方のグラフに含まれているので、それらはすべて同じ祖先を持っており、mxはどのメッセージの祖先にもなれないことになります。したがって、mxはどちらのローカルDAGでもメッセージに到達できません。したがって、祖先はs＋1で0に投票し、その結果、s＋2でG0Aのピボットにはならない。

このように、各コアメッセージは、ピボットであるか、経由しないかのどちらかで評価されます。重要なことは、異なる参加者からのコア・メッセージは、あるメッセージがピボットであるかどうかについて、すべて同意が示されていることです。これらのピボットは、DAG内のメッセージの順序を決定するために使用されます。

確認

各メッセージには、最終的にオーダー番号が付けられます。これを計算するためには、問題のメッセージと同じかそれより小さいスロットを持つすべてのコア・メッセージについて、ピボット関数が決定されていなければなりません。そして、オーダー関数のドメインは次のように与えられます。

つまり、これらはオーダー番号が計算できるメッセージであり、以下のように決定されます。

定義 3.18. オーダー番号 メッセージ mx のオーダー番号は、オーダー関数 oA : D ! N, 8A 2 V であり、次のように定義される。

ここで、s = mint2N [mz] = t , mx 2anc(mz), (mz) = 1;mz =2 Fz 8z 2 Ux; 8Ux 2 UxとDは14で定義される。

因果順序は、決定論的順序付けプロセスによって計算される。

このように、メッセージはまず順序番号でソートされ、次に因果順序でソートされ、最終的には必要に応じてハッシュでソートされます。次の定理は、すべてのメッセージに順序番号が割り当てられることを保証し、メッセージの順序付けが達成されることを保証しています。

Theorem 3.9 (Message ordering). 無傷の参加者xが作成した各メッセージm(n)xは、最終的にメッセージの全順序の中で、確率1で順序番号が割り当てられる。

品行方正な参加者xが作成したメッセージm(n)xを考えてみましょう。品行方正であるがゆえに、頻繁に同期し、仮定2.2により、これらのメッセージは最終的に配信されます。したがって、xとクォーラムが交差する参加者の中で、すべての品行方正な参加者は、最終的にm(n)xを知ります。 したがって、xとクォーラムが交差する参加者によるすべてのユニークピボットがm(n)xの子孫であるスロット（s0とする）が最終的に存在になります。

このことは、m(n)xがそのスロット内で順序番号s（因果的順序も）を割り当てられるのに十分である。歴史上のそのコンセンサスの場所は固定される。さらに、後になって、m(n)xよりも先にコンセンサス順になる新しいメッセージmyを発見できません。

確かに、合意形成の歴史の中で先に来るためには、myのオーダー番号がs以下でなければなりません。そのためには、スロットsのすべてのピボットがmyを受け取っていなければなりません。しかし、あるスロットのピボットのセットがわかってしまうと、そのピボットの祖先もすべてわかってしまい、将来DAGが大きくなったときに、そのピボットの新しい祖先を発見する方法がありません。さらに、あるスロットの既知のコアメッセージがすべてピボットであるかどうか決定されると、そのスロットが将来的に新しいピボットを獲得できません。

作成者が既知のスロットs＋1個のコアメッセージの作成者と定足数交点を持つ新しいスロットsのコアメッセージが将来発見されても、既知のスロットs＋1個のコアメッセージの祖先にはなりません。つまり、スロットs＋1のコアメッセージのどのクォーラムでも強く到達できないので、ピボットではないというコンセンサスがすぐに得られる。したがって、一旦メッセージが全体の順序の中で場所を割り当てられると、他の既知のメッセージと交換しても、後から発見された新しいメッセージがその前に挿入されても、その位置は決して変わりません。

結論

Flare Consensus Protocol (FCP)は、簡略化された公正なFederated Byzantine Agreement (FBA)構築である。Flare Consensus Protocol (FCP)はFBA協定の文脈の中に存在し、Hashgraphによって導入された仮想投票を効果的に一般化したものです。Flare Consensus Protocol (FCP)をHashgraph、SCP、Blockmaniaと比較します。

ネットワークに固定数の参加者Nがいるとします。それぞれの参加者が定足数のスライスを(2N + 1)=3人の参加者のすべての組み合わせに設定した場合、つまり、各メンバーのスライスのセットにそのメンバー自身が含まれるような場合、この特別なケースはHashgraph Consensus Protocolに戻ります。ハッシュグラフ・コンセンサス・プロトコルは、この(2N + 1)/3の構成、すなわち伝統的なビザンチン合意においてのみ存在でき、本質的にSybil攻撃を克服できません。Flareコンセンサスプロトコルは、Federated Byzantine Agreementの枠組みの中に存在し、参加者が独立してクォーラムスライスの決定できるため、Sybil攻撃を本質的に克服しています。

Blockmaniaは、PBFTフレームワークで構成された伝統的なビザンチン合意のコンセンサスプロトコルで、Hashgraph Consensus Protocolで確立された仮想投票技術を利用して、通常のPBFTよりも通信量を大幅に削減しています。
通常のPBFTよりも通信量を大幅に削減できます。

Flare Consensus Protocolは、Federated Virtual Voting技術により、投票ベースのアプローチ（Stellar Consensus Protocolなど）と比較して、通信量の大幅な削減を実現しています。ステラコンセンサスプロトコルもリーダーベースで、リーダー候補がFederated Byzantine Agreement (FBA)ネットワーク内でどれだけ中心に位置しているかでリーダーを選択します。これにより、ネットワークの周辺に存在する参加者は、ネットワーク内で最小限の力しか持たないため、多数の参加者がコンセンサスに与える影響を大幅に抑えられます。

一方、Flare Consensus Protocol (FCP)は、完全にリーダー不在であり、ネットワーク上の参加者数の増加に応じて直接ネットワークを公平にコントロールできます。これは、ダークプール取引などの多くの場面で公平性を実現するために非常に重要です。

Flare Consensus Protocol (FCP)は、ステラコンセンサスプロトコル論文で確立されたFederated Byzantine Agreement（連邦ビザンチン合意）の表記法と理論的保証を活用して、Federated Virtual Voting(仮想投票連合)を導入するものです。Flare Consensus Protocol (FCP)は、簡略化された公正なFederated Byzantine agreementの構築であり、Byzantine Fault Toleranceが証明されています。これらの特性により、Flare Consensus Protocol (FCP)はインターネットレベルのチューリング完全合意の有力なモデルとなっています。